Utilizzo del modello per la determinazione dell’acqua interagente nel calcolo dei rendimenti delle operazioni di lavaggio

Utilizzo del modello per la determinazione dell’acqua interagente nel calcolo dei rendimenti delle operazioni di lavaggio – Parte B

 

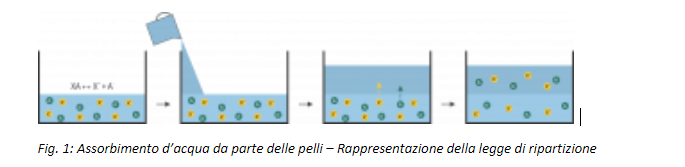
I lavaggi vanno considerati come vere e proprie operazioni il cui scopo è quello di pulire le pelli da ciò che resta dei bagni esausti di fine lavorazione. 

Possono avere anche lo scopo di riscaldare o raffreddare le pelli, ma si tratta sempre di uno scopo sinergico a quello della pulizia. Seguono i principi delle estrazioni chimiche e la teoria della ripartizione chimica ci aiuta a capire cosa succede durante le fasi di pulizia per il cui calcolo dei rendimenti è necessaria la conoscenza dei volumi d’acqua coinvolti, che sono i volumi dei bagni di lavaggio ed i volumi di acqua interagente nelle pelli.  Sono stati precedentemente forniti gli strumenti per stimare quest’ultimo dato. Si fornisce infine una proposta di correzione delle formule per avvicinare i risultati teorici a quelli della pratica reale. 

 

Breve introduzione alla teoria della ripartizione chimica 

Immaginiamo di avere un sistema chiuso che contiene un soluto generico sciolto in un solvente A al quale addizioniamo un secondo solvente B tale per cui: 

• I solventi A e B sono immiscibili tra loro; 
• Il soluto è miscibile sia in A che in B. 

Una volta aggiunto B, il soluto inizia a spostarsi da A a B e la diffusione si arresta una volta raggiunto l’equilibrio delle concentrazioni. 

La forza motrice del processo è la differenza di potenziale chimico (potenziale diffusivo) che il soluto presenta nelle due fasi (solvente + soluto) rispetto alle condizioni di equilibrio (in cui il potenziale diffusivo è nullo): 

 

 

La causa della diffusione è l’affinità che il soluto presenta nei confronti del secondo solvente B. 

Inizialmente nella fase A il potenziale chimico è massimo mentre nella fase B zero, la differenza di potenziale è massima e il soluto diffonde da A a B con rapidità. La velocità di diffusione decresce fino ad annullarsi una volta raggiunto l’equilibrio:  

 

Vi è pur sempre uno scambio di soluto tra i due solventi, ma la causa non è il gradiente chimico. 

Nelle equazione: 

• µA,B = potenziale chimico del soluto nella fase A o B; 
• µ0A,B = potenziale chimico del soluto nelle due fasi in condizioni standard; 
• aA,B = attività del soluto nella fase A o B. 

All’equilibrio i potenziali del soluto nelle due fasi si equivalgono (μA=μB) perchè la loro differenza è nulla: 

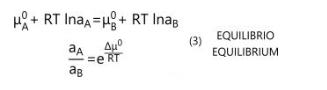
Nella (3) l’unica variabile è la temperatura. Se questa è costante (cosa che si può supporre vera nella pratica di conceria), la (3) si può esprimere come Legge di distribuzione di Nernst che regola i processi di estrazione liquido-liquido. Questa legge ci dice che, all’equilibrio, il rapporto tra le attività di un soluto distribuito fra due liquidi tra loro immiscibili è costante a temperatura costante: 

 

La (4) fa riferimento alle attività dei soluti, che non sono altro che i valori delle concentrazioni che riescono a partecipare effettivamente ai fenomeni che vengono descritti. L’attività viene presa in considerazione quando si lavora con soluzioni concentrate perché gli ioni sono soggetti anche a fenomeni di interazione reciproci che ne limitano le concentrazioni disponibili. Quando si lavora con sistemi diluiti, cosa spesso valida nella pratica conciaria (e a maggior ragione durante i lavaggi), possiamo lavorare con le concentrazioni e la (4) viene espressa secondo la (5): 

La costante K viene chiamata costante di ripartizione. È indipendente dai volumi di solvente usati e dipende solo dalla temperatura in cui si trova il sistema. Questa condizione è sempre una condizione ideale perchè nei casi reali K non ha andamento lineare ma curvo. 

Applicazione della teoria della ripartizione chimica alla pratica conciaria 

Il presente capitolo è costruito sviluppando le lezioni del Prof. A. Ballardin, che è stato docente presso l’ITTE G. Galilei di Arzignano ed al quale va sempre il nostro personale e commosso ricordo. 

Possiamo considerare le fasi di lavaggio come delle estrazioni liquido-liquido in cui: 

• il primo liquido è costituito dal bagno trattenuto all’interno delle pelli; 

• il liquido estraente è costituito dal bagno di lavaggio. 

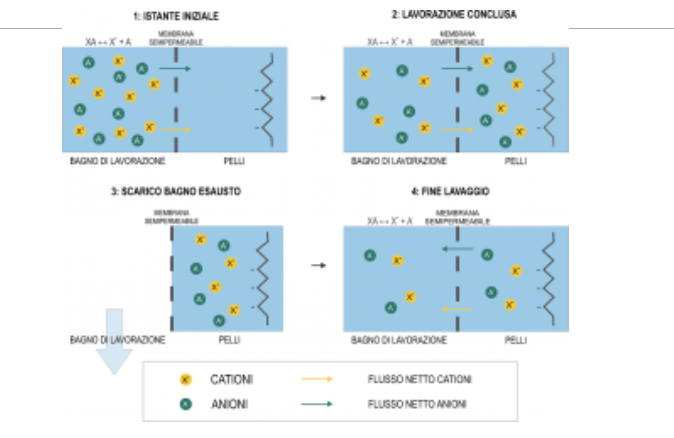
Figura 2: Assorbimento d’acqua da parte delle pelli – Modello di membrana semipermeabile e fase di lavaggio 

Se usiamo il modello della membrana semipermeabile possiamo considerare i volumi di questi due fluidi come volumi che rimangono separati.    

Andiamo a vedere in dettaglio cosa succede, utilizzando il termine generico di soluti per indicare i prodotti chimici residui che devono essere puliti, ovvero: 

• Le sostanze che non sono riuscite a legarsi alle pelli e che possono essere considerate alla stregua di impurità (specie dopo acidificazione); 
• Le sostanze debolmente legate alle pelli e che sono disponibili ad essere solvatate. 

Assumeremo che questi siano completamente solubili, approssimazione che può essere considerata valida per via dell’agitazione continua dei bagni. 

Definiamo: 

• c0 concentrazione iniziale di soluto nel bagno di lavorazione; 

• cP concentrazione del soluto nella pelle (bagno esausto) alle condizioni di equilibrio; 
• cB concentrazione del soluto nel bagno di lavaggio alle condizioni di equilibrio; 
• LP liquido contenuto all’interno delle pelli alle condizioni di massima idratazione (bagno esausto); 
• VP=V0 volume di LP (il volume d’acqua contenuto nelle pelli); 
• LB liquido contenuto nel bagno di lavaggio (liquido estraente); 

• VB volume del bagno di lavaggio LB (liquido estraente); 
• K coefficiente di estrazione. 

L’agitazione dei bottali incrementa le velocità di estrazione. Non vi è solo il contributo del rimescolamento, ma anche quello della continua compressione e rilascio delle pelli che vengono invogliate meccanicamente a perdere e a riacquistare acqua. Nei lavaggi possiamo considerare che 10-15 minuti siano sufficienti per raggiungere gli equilibri di concentrazione. 

All’equilibrio i flussi d’acqua in entrata ed uscita dalle pelli sono uguali e bilanciati. I soluti si ripartiscono rispettando i rispettivi coefficienti di ripartizione K (6). Ciascuno di essi, nel caso del sistema pelle-bagno, diventa: 

Un bilancio di massa relativo ai soluti ci dice che, una volta raggiunto l’equilibrio, la massa iniziale dei soluti (ovvero quella presente all’interno delle pelli), si distribuisce tra i due volumi d’acqua secondo quanto afferma la legge di ripartizione: 

Esplicitando cP e passando dalle concentrazioni alle masse, poiché VP=V0, e poichè quantità dei soluti estratte dalle pelli è pari a me = mB = m0 – mP, si ricava: 

Definendo il rendimento di un’estrazione come il rapporto tra la massa estratta e la massa iniziale, si ottiene la (8): 

Poiché si fa riferimento allo stesso solvente, che è sempre acqua, il valore di K è pari ad 1 e la (8) si semplifica nella (9): 

K è pari ad uno perchè i due liquidi sono sempre gli stessi. Il fatto che uno di essi sia sporco mentre l’altro sia pulito, non incide su come si distribuiscono i soluti all’equilibrio ma incide solo sulle velocità con cui gli equilibri vengono raggiunti.   

La (9) fornisce il rendimento di una singola operazione di lavaggio, che è determinato unicamente dal rapporto dei due volumi d’acqua VP e VB e cresce all’aumentare di VB. 

Quando i lavaggi sono due o in numero superiore, parliamo di lavaggi multipli. In questi casi, i rendimenti complessivi di n lavaggi sono dati dalla somma dei rendimenti di ciascun lavaggio singolo:  

Nella (10) i rendimenti dei lavaggi successivi al primo devono essere calcolati sulle quantità di soluti residue e non sulle quantità iniziali. 

Nei lavaggi multipli sono eseguiti con il medesimo rapporto bagno, la (9) diventa: 

 

Come vediamo nelle formule (8), (9) e (10), i rendimenti dei lavaggi dipendono dai volumi d’acqua coinvolti. 

Per la determinazione di VP è stato messo a punto il modello per il calcolo dell’acqua interagente precedentemente illustrato. Il valore di questo termine è costante e non viene deciso dall’operatore. 

I volumi d’acqua trattenuti dalle pelli hanno valori elevati e le concentrazioni degli inquinanti trattenuti sono le stesse di quelle scaricate con i bagni esausti delle operazioni che precedono il lavaggio. Nel caso di lavaggi multipli è possibile che l’operazione precedente sia un lavaggio stesso. Come abbiamo visto sempre in precedenza, la quantità di acqua interagente è maggiore nel caso delle operazioni vere e proprie ed è minore nei lavaggi perché i tempi di diffusione del solvente sono inferiori. 

VB rappresenta l’acqua introdotta nel bottale i cui volumi vengono decisi dagli operatori. E’ corretto dire che i rendimenti dei lavaggi, benché dipendano dai volumi d’acqua coinvolti, sono funzione dei rapporti bagno impiegati: 

R=f(VB) 

Questi ultimi (8) hanno incrementi significativi fino a RB del 200-250%. Oltre a queste percentuali, gli incrementi delle rese estrattive sono modesti e non giustificati dall’incremento dei volumi d’acqua, come mostra il Grafico 1: 

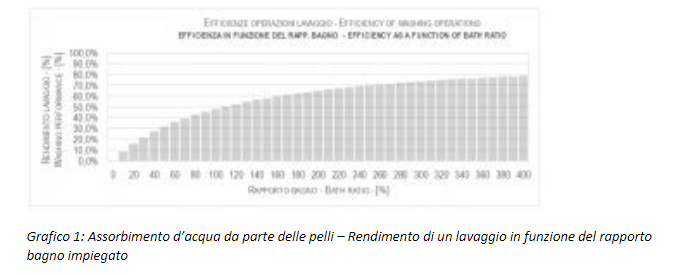
I rendimenti complessivi dei lavaggi multipli sono dati dalla somma dei rendimenti di ciascun lavaggio singolo, come specificato nella (9). Gli incrementi nei rendimenti non sono così alti come ci si aspetterebbe perché devono essere calcolati sulle quantità di inquinanti rimanenti e non su quelle iniziali. 

Molto spesso, nei lavaggi multipli i rapporti bagno rimangono gli stessi, semplificando notevolmente i calcoli (10). Alcuni esempi di rendimento di lavaggi singoli e multipli con rapporti bagno costanti sono riportati nella Tabella 1, che riporta un elenco dei rendimenti teorici per lavaggi singoli (I°) e multipli (II° e III°), calcolati tutti per mezzo delle (9) e (11): 

Quanto visto fino a questo momento fa riferimento a casi teorici. I valori dei rendimenti reali sono diversi ed oscillano attorno ai valori teorici secondo percentuali che aumentano all’aumentare del numero di lavaggi n.  

Per ricavare i rendimenti reali da quelli teorici viene proposto di introdurre nelle formule (8), (9) e (10)  dei coefficienti di correzione che sono ricavati da esperienze pratiche: 

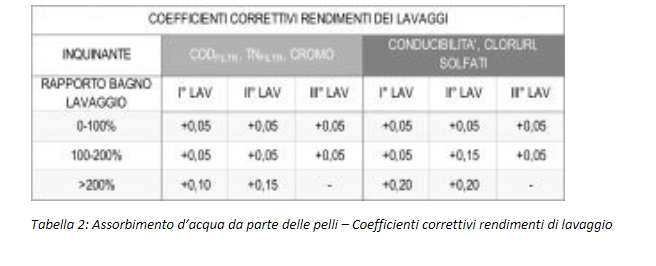
I coefficienti di correzione sono diversi a seconda dell’inquinante indagato ed in funzione dell’ordine con cui avviene il lavaggio (I°<II°<III°) e sono compresi tra 0,03 e 0,2 (ovvero tra il 3 ed il 20%). Sono riportati nella Tabella 2 che è stata costruita raccogliendo i dati di un gran numero di prove sperimentali: 

A cura di 

Marco Nogarole, Responsabile del Trasferimento Tecnologico della SSIP

in collaborazione con l’Ing. Daniele Pistorio

Pubblicato il: 28 Lug 2022 alle 14:41